Ontwikkeling van de quantummechanica

• 
• 

Gegevens

Gemaakt op vrijdag 08 augustus 2025 23:10

Laatst bijgewerkt op woensdag 27 augustus 2025 23:39

Gepubliceerd op vrijdag 08 augustus 2025 23:13

Hits: 152

Quantummechanica is de natuurkunde die zich bezig houdt met bestudering van de bewegingen van de allerkleinste onderdelen of quanta van materie: atomen, electronen, protonen, neutronen, fotonen quarks, neutrino's etcetera. Energie bestaat volgens de quantummechanica uit kleine pakketjes, de zogenaamde quanta. Volgens de quantummechanica kan de postie van quanta niet voorspeld worden. Er kan alleen een bepaalde kans of waarschijnlijkheid berekend worden waar het quantum wordt aangetroffen. Wij kunnen bijvoorbeeld niet de positie van een elektron t.o.v. de kern van het atoom vaststellen. Een elektron kan zich namelijk op meerdere posites tegelijk bevinden.

Belangrijke bijdragen aan de quantummechanica

Max planck(1900)

Bijdrage: Max Planck nam aan dat energie niet continu is, maar uit kleine discrete pakketjes—quanta—bestaat. Hij kwam tot deze aanname bij het oplossen van het al langer bestaande probleem van de zwarte straler: (voorbeelden van zwarte stralers zijn o.a. een ovenopening of het wolfraamdraadje van een gloeilamp). Deze objecten absorberen alle straling en bij verwarming zenden zij straling uit met een spectrum dat alleen van de temperatuur afhangt.
Het probleem: De klassieke natuurkunde (Rayleigh–Jeans) voorspelde dat bij hoge frequenties de stralingsintensiteit onbeperkt zou toenemen (de ultravioletcatastrofe). Metingen lieten echter zien dat de intensiteit bij hogere frequenties juist sterk afneemt (zoals in de wet van Wien).

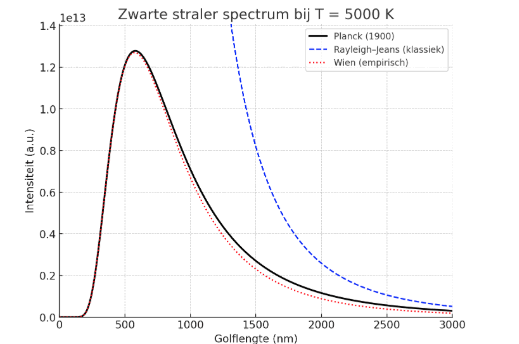
Plancks oplossing. Planck beschreef de meetgegevens wiskundig en kon ze alleen verklaren door te veronderstellen dat de energie van de trillende elektromagnetische oscillatoren in de wanden van de zwarte straler gekwantiseerd is:

E=nhν

waarbij
n = geheel getal (0, 1, 2, …)
ν = trillingsfrequentie
h = Planck-constante (bepaalt de grootte van een energiekwantum) Deze aanname voorkomt de ultravioletcatastrofe en opende de deur naar de quantummechanica.

Albert Einstein(1905)

Bijdrage: Stelde dat Licht bestaat uit kleine energiedeeltjes (fotonen), die in staat zijn elektronen uit metaal vrij te maken of te slaan: het zogenaamde fotoelektrisch effect.

Niels Bohr(1913)

Bijdrage: Paste het idee van Planck toe in zijn atoommodel door te stellen dat negatief geladen elektronen alleen in bepaalde(discrete) energiebanen rond de positief geladen atoomkern kunnen zijn en slechts van baan kunnen veranderen door door een discrete foton(quantum) uit te zenden of te absorberen.
Dit verklaarde voor het waterstofatoom de spectrumlijnen van Balmer en Rydberg.
Zijn voorgestelde berekening werkte echter niet bij atomen met meer dan een elektron.

1916 – Arnold Sommerfeld: Uitbreiding van het Bohr-model

Bijdrage: Elektronenbanen kunnen elliptisch zijn, niet alleen cirkelvormig.
Gevolg: Betere verklaring van spectra van atomen.
Zijn voorgestelde benadering werkte echter ook niet bij atomen met meer dan een elektron.
Termen:
Elliptische baan: Een uitgerekte cirkelvormige baan.
Spectrumlijnen: De gekleurde lijnen die ontstaan als atomen licht uitzenden of absorberen.

1923 – Louis de Broglie: Golven van materie

Bijdrage: Materie, zoals elektronen, kan zich ook gedragen als een golf.
Termen:
Golflengte: De afstand tussen twee opeenvolgende golftoppen.
Dualiteit: Het idee dat iets zowel golf- als deeltjesgedrag kan vertonen.

1924 – Satyendra Nath Bose & Einstein: Bose-Einstein-statistiek

Bijdrage: Wiskundige beschrijving van deeltjes die in dezelfde toestand kunnen bestaan.
Toepassing: Voorspelling van het Bose-Einstein-condensaat (een nieuwe aggregatietoestand bij extreem lage temperaturen).
Termen:
Statistiek: Wiskundige beschrijving van hoe deeltjes zich verdelen over energieniveaus.
Condensaat: Een toestand waarin veel deeltjes exact dezelfde kwantumtoestand hebben.

Werner Heisenberg (1925)

Bijdrage: Ontwikkelde matrixmechanica, de eerste versie van de quantummechanica.

Grondidee: Je kunt de positie (x) en impuls (p) van een deeltje nooit allebei exact meten.

Vergelijking (Onzekerheidsprincipe):

Δx ⋅ Δp ≥ ℏ / 2

Symbolen:

• Δx = onzekerheid in positie
• Δp = onzekerheid in impuls
• ℏ = gereduceerde Planckconstante (ℏ)
• ℏ = h / (2π)
• h = Planckconstante (≈ 6,626 × 10^-34 J·s)

2. Erwin Schrödinger (1926)

i ℏ (∂ψ / ∂t) = Ĥ ψ

• i = imaginaire eenheid (i² = −1)
• ℏ = gereduceerde Planckconstante
• ψ (psi) = golffunctie → bevat alle informatie over de toestand van het systeem
• ∂/∂t = afgeleide naar tijd
• Ĥ = Hamilton-operator → totale energie van het systeem

3. Paul Dirac (1928)

(i γμ ∂μ − m) ψ = 0

• i = imaginaire eenheid
• γμ = gamma-matrices (4×4 matrices die relativistische eigenschappen coderen)
• ∂μ = afgeleide naar tijd en ruimte (4-vector)
• m = massa van het deeltje
• ψ = 4-componentige spinor (relativistische golffunctie)

Deze vergelijking voorspelde antimaterie (o.a. het positron).

4. Richard Feynman, Julian Schwinger, Sin-Itiro Tomonaga (1940s)

Lint = − e ψ̄ γμ Aμ ψ

• e = elektrische lading
• ψ̄ = geconjugeerde golffunctie (Dirac-adjunct)
• Aμ = elektromagnetisch veld
• γμ = gamma-matrices
• Lint = interactie-Lagrangiaan

5. Murray Gell‑Mann (1960s–70s)

LQCD = ψ̄ (i γμ Dμ − m) ψ − 1/4 Gμνa Gaμν

• Dμ = covariante afgeleide met gluonvelden
• Gμνa = veldsterkte-tensor van gluonen
• a = kleurindex (er zijn 8 mogelijke gluonen)

6. Sheldon Glashow, Abdus Salam, Steven Weinberg (1960s)

Symmetrie: SU(2) × U(1)
L ⊃ − 1/4 Wμνa Waμν − 1/4 Bμν Bμν + …

• Wμνa = veldsterkte van de W‑bosonen
• Bμν = veldsterkte van het hyperladingveld
• SU(2) en U(1) = wiskundige symmetriegroepen

7. Yoichiro Nambu (1960s) — Spontane symmetriebreking

Voorbeeld idee: V(φ) = μ^2 |φ|^2 + λ |φ|^4  (μ^2 < 0 geeft breking, veld krijgt v = ⟨φ⟩ ≠ 0)

8. Peter Higgs, François Englert & Robert Brout (1964) — Higgs-mechanisme

Massaterm (vereenvoudigd): m_W ∝ g v  (v = vacuum expectation value van Higgsveld)

9. Gerard ’t Hooft & Martinus Veltman (1970s)

10. Kenneth G. Wilson (1970s) — Renormalisatiegroep & lattice methoden

11. David Gross, Frank Wilczek & David Politzer (1970s)

Gedrag van de koppeling: β(g) < 0 → g(μ) ↓ als μ ↑

12. Makoto Kobayashi & Toshihide Maskawa (1973)

13. Yoichiro Nambu, Kobayashi & Maskawa — Nobelprijzen 2008 (delen)

14. Gerard ’t Hooft & Martinus J. G. Veltman — Nobelprijzen en precisiewerk

15. Kenneth Lane, Michael Creutz e.a. — Niet-perturbatieve methoden en lattice-gemeenschap (1970s→heden)

16. Edward Witten (1980s→heden) — Mathematische inzichten & QFT

17. Juan Maldacena (1997) — AdS/CFT correspondentie

18. Experimentele bevestigingen (belangrijke gebeurtenissen)

• Ontdekking W- en Z-bosonen (CERN, 1983) — bevestiging elektrozwakke theorie.
• Ontdekking top-quark (Fermilab, 1995) — bevestiging derde generatie.
• Observatie van het Higgsboson (CERN, 2012) — bevestiging Higgs-mechanisme.

19. Recente/actuele gebieden (samenvatting)

• Niet-perturbatieve QFT (lattice QCD, numerieke technieken).
• Topologische en conformele veldtheorieën — invloed op zowel wiskunde als fysica.
• Dualiteiten (AdS/CFT), sterke-zwakke koppelingstechnieken.
• Zoeken naar uitbreiding van het standaardmodel: neutrino-eigenschappen, donkere materie, en quantum zwaartekracht (string theory / loop quantum gravity).

Belangrijke formules & concepten (kort)

• Higgs-potentiaal (voorbeeld): V(φ) = μ^2 |φ|^2 + λ |φ|^4 → bij μ^2 < 0: ⟨φ⟩ = v ≠ 0
• QCD Lagrangiaan (vereenvoudigd):

  ℒ_QCD = ψ̄(iγ^μ D_μ - m)ψ  − (1/4) G^a_{μν} G^{aμν}

• Renormalisatie groep (schematisch): μ (schaling) → g(μ), met β(g)=μ dg/dμ
• Asymptotic freedom: β(g) < 0 voor QCD → koppeling wordt kleiner op hoge energieën

Uitleg van belangrijke symbolen gebruikt hierboven

• φ (phi) — scalar veld (bv. Higgsveld).
• V(φ) — potentiaal van een veld; bepaalt stabiele/vacuum-staten.
• ⟨φ⟩ = v — vacuum expectation value (vev): gemiddelde waarde van het veld in de grondtoestand.
• ψ, ψ̄ — fermionveld en diens Dirac-conjugaat (bv. quarks, elektronen).
• γ^μ — gamma-matrices (relativistische spinstructuur, μ = 0,1,2,3).
• D_μ — covariante afgeleide: D_μ = ∂_μ + i g A^a_μ T^a (voegt interacties toe met gaugevelden).
• G^a_{μν} — veldtensor van gluonen (QCD); a = kleurindex.
• ℒ — Lagrangedichtheid: compacte expressie die de dynamica van velden bepaalt.
• β(g) — beta-functie; beschrijft hoe de koppelingsconstante g verandert met energie-schaal μ.

Samenvattende tabel  personen & kernbijdragen:

Betekenis:Continu betekent dat een grootheid elke willekeurige waarde kan aannemen, zonder sprongen of onderbrekingen.

Voorbeeld: in energie: als energie continu verdeeld zou zijn, kan een oscillator (zoals een trilling in een zwarte straler) energie hebben van 1,01 J, 1,011 J, 1,0111 J, enzovoort – er is geen beperking, elke kleine stap is mogelijk.

Vergelijking:d: zoals water dat je uit een kraan giet: je kunt er precies 1 liter uithalen, maar ook 1,0001 liter, of elk ander willekeurig getal daartussen.

Betekenis:Betekenis: een grootheid kan alleen bepaalde afzonderlijke waarden aannemen, vaak in stapjes van een vaste grootte.
Voorbeeld: in energie (Planck): de energie van een oscillator is niet willekeurig, maar moet een veelvoud zijn van een klein pakketje ℎ. Dus alleen:

0ℎv, 2hv, 3ℎv, 4hv,....
en niet iets daartussen, zoals 2,5hν.
Vergelijking: zoals geldstukken: je kunt betalen met €1, €2, €3, maar niet met €2,37 als je alleen hele euro’s hebt.

Intensiteit is de hoeveelheid energie (spectrale intensiteit ) ofwel de hoeveelheid elektromagnetische straling, per tijdseenheid, per oppervlakte-eenheid en per frequentiegebied die een zwarte straler bij een gegeven temperatuur. per seconde uitzendt in de vorm van.
Bij lage frequenties (radiogolven, microgolven) is de intensiteit klein.
Bij een bepaalde frequentie (afhankelijk van de temperatuur) is er een maximum aan de intensiteit: dat is de kleur waarin het object het sterkst straalt (bij de zon is dat in zichtbaar licht, bij de kosmische achtergrondstraling zijn dat microgolven).
Bij hogere frequenties (ultraviolet, röntgen) neemt de intensiteit snel af.

Een voorbeeld van een zwarte straler is gloeidraad van wolfram die een temperatuur heeft van ~2726.85 Celsius. Bij deze temperatuur zend de gloeidraad veel infrarode elektromagnetische straling uit, wat de warmte verklaart. De gloeidraad zend 2-5% van het elektrisch vermogen in zichtbaar licht(400 – 700 nanometer) uit. De gloeidraad zendt bijna niet uit in het ultraviolette spectrum.

Intensiteit van straling (I) heeft direct met energie (E) te maken:
Energie (E): de totale hoeveelheid stralingsenergie die wordt uitgezonden.
Intensiteit (I): Afgeronde hoeveelheid energie(d) per seconde I(ν,T)∼ dE/dtdAdν

Het foto-elektrisch effect werd in 1905 door Albert Einstein met een formule verklaard. Volgens Einstein bestaat licht uit afgeronde pakketjes energie van gelijke grootte: de fotonen.
Wanneer fotonen(lichtdeeltjes) op een metaal vallen, kunnen ze elektronen losmaken. Hoe meer licht (dus hoe meer fotonen), hoe meer elektronen er vrijkomen.
De energie van de vrijgekomen elektronen hangt niet af van de hoeveelheid licht, maar van de soort (kleur) van het licht.
Blauwe fotonen dragen meer energie dan rode fotonen. Daarom krijgen de elektronen die door blauw licht worden vrijgemaakt meer energie mee dan de elektronen die door rood licht vrijkomen.

Einstein gebruikte in 1905 de volgende formule om het foto-elektrisch effect te verklaren:

E_kin =h⋅f−W

E_kin = de kinetische energie van het vrijgekomen elektron
h = de constante van Planck (6,626×10⁻³⁴\cdotps)
f= de frequentie van het invallende licht
W = de uittreedarbeid (de minimale energie die nodig is om een elektron uit het metaal los te maken)